| <— 1.1 Навчання на основі даних | Зміст | 1_3_Under_and_overfitting —> |
1.2 Регресія на основі базисних функцій
Ми можемо проілюструвати тренування моделі на простому прикладі, де $x_n$ і $y_n$ є двома дійсними числами, втрата - це середнє квадратичне відхилення (mean squared error): \(\mathscr{L}(w)=\frac{1}{N}\sum_{n=1}^N(y_n-f(x_n;w))^2 \tag{1.1}\)
і $f(\cdot;w)$ є лінійною комбінацією попередньо означеного базису функцій $f_1,…,f_K$, з $w=(w_1,…,w_K)$:
\[f(x;w)=\sum_{k=1}^Kw_kf_k(x)\]Оскільки $f(x_n;w)$ є лінійною відносно параметрів $w_k$, а $\mathscr{L}(w)$ є квадратичною відносно $f(x_n;w)$, функція втрат $\mathscr{L}(w)$ є квадратичною по відношенню до параметрів $w_k$. Тому пошук $w^*$, які мінімізують функцію втрат, зводиться до вирішення лінійної системи. Дивіться рис. 1.1 для прикладу з Гаусовими ядрами (Gaussian kernels) як $f_k$.
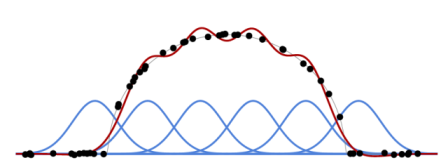
Рисунок 1.1: На основі базисних функцій (сині криві) і тренувального набору (чорні крапки), ми можемо обчислити оптимальну лінійну комбінацію (суму) цих базисних функцій(червона крива), щоб наблизити навчальний набір даних за середнім квадратичним відхиленням.